DocumentCode :
745834
Title :
The rank and kernel of extended 1-perfect Z4-linear and additive non-Z4-linear codes
Author :
Borges, Joaquim ; Phelps, Kevin T. ; Rifà, Josep
Author_Institution :
Comput. Sci. Dept., Univ. Autonoma de Barcelona, Bellaterra, Spain
Volume :
49
Issue :
8
fYear :
2003
Firstpage :
2028
Lastpage :
2034
Abstract :
A binary extended 1-perfect code of length n + 1 = 2t is additive if it is a subgroup of Z2α × Z4β. The punctured code by deleting a Z2 coordinate (if there is one) gives a perfect additive code. 1-perfect additive codes were completely characterized and by using that characterization we compute the possible parameters α, β, rank, and dimension of the kernel for extended 1-perfect additive codes. A very special case is that of extended 1-perfect Z4-linear codes.
Keywords :
binary codes; linear codes; 1-perfect additive codes; additive non-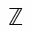 4-linear codes; binary extended 1-perfect code; dimension; extended 1-perfect
4-linear codes; binary extended 1-perfect code; dimension; extended 1-perfect 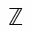 4-linear code; kernel; punctured code; rank; subgroup; Additives; Arithmetic; Binary codes; Combinatorial mathematics; Computer science; Hamming distance; Kernel; Linear code; Propulsion;
4-linear code; kernel; punctured code; rank; subgroup; Additives; Arithmetic; Binary codes; Combinatorial mathematics; Computer science; Hamming distance; Kernel; Linear code; Propulsion;
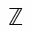 4-linear codes; binary extended 1-perfect code; dimension; extended 1-perfect
4-linear codes; binary extended 1-perfect code; dimension; extended 1-perfect 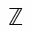 4-linear code; kernel; punctured code; rank; subgroup; Additives; Arithmetic; Binary codes; Combinatorial mathematics; Computer science; Hamming distance; Kernel; Linear code; Propulsion;
4-linear code; kernel; punctured code; rank; subgroup; Additives; Arithmetic; Binary codes; Combinatorial mathematics; Computer science; Hamming distance; Kernel; Linear code; Propulsion;fLanguage :
English
Journal_Title :
Information Theory, IEEE Transactions on
Publisher :
ieee
ISSN :
0018-9448
Type :
jour
DOI :
10.1109/TIT.2003.814490
Filename :
1214081
Link To Document :
