DocumentCode :
862137
Title :
R+ fading memory and extensions of input-output maps
Author :
Sandberg, Irwin W.
Author_Institution :
Dept. of Electr. & Comput. Eng., Texas Univ., Austin, TX, USA
Volume :
49
Issue :
11
fYear :
2002
fDate :
11/1/2002 12:00:00 AM
Firstpage :
1586
Lastpage :
1591
Abstract :
Much is known about time-invariant nonlinear systems with inputs and outputs defined on R+ that possess approximately finite memory. For example, under mild additional conditions, they can be approximated arbitrarily well by the maps of certain interesting simple structures. An important fact that gives meaning to results concerning such systems is that the approximately finite memory condition is known to be often met. Here we consider the known proposition that if a causal time-invariant continuous-time input-output map H has fading memory on a certain set of bounded functions defined on all of R, then H can be approximated arbitrarily well by a finite Volterra series operator. We show that in a certain sense, involving the existence of extensions of system maps, this result too has wide applicability.
Keywords :
Volterra series; continuous time systems; nonlinear systems; 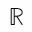 + fading memory; Volterra series operator; approximately finite memory; causal time-invariant continuous-time input-output map; nonlinear system; system map extension; Fading; Helium; Image processing; Lattices; Multi-layer neural network; Neural networks; Nonlinear systems; Radial basis function networks; Stability criteria;
+ fading memory; Volterra series operator; approximately finite memory; causal time-invariant continuous-time input-output map; nonlinear system; system map extension; Fading; Helium; Image processing; Lattices; Multi-layer neural network; Neural networks; Nonlinear systems; Radial basis function networks; Stability criteria;
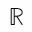 + fading memory; Volterra series operator; approximately finite memory; causal time-invariant continuous-time input-output map; nonlinear system; system map extension; Fading; Helium; Image processing; Lattices; Multi-layer neural network; Neural networks; Nonlinear systems; Radial basis function networks; Stability criteria;
+ fading memory; Volterra series operator; approximately finite memory; causal time-invariant continuous-time input-output map; nonlinear system; system map extension; Fading; Helium; Image processing; Lattices; Multi-layer neural network; Neural networks; Nonlinear systems; Radial basis function networks; Stability criteria;fLanguage :
English
Journal_Title :
Circuits and Systems I: Fundamental Theory and Applications, IEEE Transactions on
Publisher :
ieee
ISSN :
1057-7122
Type :
jour
DOI :
10.1109/TCSI.2002.804547
Filename :
1046827
Link To Document :
